本文介绍了从基础到进阶的数学探索,重点在于排列公式的推导。介绍了排列的基本概念和性质,包括排列的定义、性质和计算方法。通过具体例子和图示,逐步推导了排列公式的计算过程,包括阶乘的定义、性质和计算方法,以及排列公式的推导和应用。在进阶部分,介绍了排列公式的扩展应用,如错排公式的推导和计算方法,以及排列组合在组合数学中的应用。通过实例分析和练习题,帮助读者巩固所学知识,提高解决实际问题的能力。本文旨在为读者提供从基础到进阶的数学探索,帮助读者深入理解排列公式的本质和应用。
在数学的广阔天地中,排列公式作为组合数学的一个重要分支,不仅在理论研究中占据一席之地,也在实际应用中发挥着不可替代的作用,从日常生活中的日程安排到复杂的计算机算法设计,排列公式的应用无处不在,本文将带领读者从基础概念出发,逐步推导排列公式,并探讨其在不同领域中的应用,以期为读者提供一次深入而有趣的数学探索之旅。
一、基础概念:何为排列?
排列(Permutation)是指从n个不同元素中取出m(m≤n)个元素,按照一定的顺序进行排列的方式,简而言之,就是考虑元素的“顺序”进行组合的过程,从“ABC”三个字母中选取两个进行排列,可以得到“AB”、“AC”、“BA”、“CA”和“CB”五种不同的排列方式。
二、排列公式的直观理解
在理解排列公式的推导之前,我们先通过一个简单的例子来直观感受其含义,假设有n个不同的元素,我们想要从中选出r个元素进行排列,我们选择第一个位置上的元素,有n种选择;接着选择第二个位置上的元素,由于已经选了一个元素放在第一个位置上,所以现在只剩下n-1种选择;以此类推,直到最后一个位置上的元素只有1种选择,总的排列方式为n×(n-1)×...×(n-r+1),这个连乘式就是排列公式的基础形式。
三、排列公式的数学推导
正式的数学推导过程如下:
设P(n, r)表示从n个不同元素中取出r个元素进行排列的数目,根据定义,我们可以考虑以下几种情况:
1、当r=0时:P(n, 0) = 1,即从n个元素中选取0个元素进行排列的方式只有一种,即什么都不选。
2、当r=1时:P(n, 1) = n,即从n个元素中选取1个元素进行排列的方式有n种。
3、对于r>1的情况:考虑第一个位置有n种选择,第二个位置有n-1种选择(因为第一个位置已经选了一个),以此类推,直到最后一个位置只有1种选择,总的排列数为:
\[ P(n, r) = n \times (n-1) \times (n-2) \times \cdots \times (n-r+1) \]
这个连乘式可以表示为:
\[ P(n, r) = \frac{n!}{(n-r)!} \]
!”表示阶乘,即n! = n × (n-1) × ... × 2 × 1。
四、排列公式的性质与证明
性质一:P(n, r) = P(n, n-r)
这个性质表明从n个元素中选取r个元素进行排列的方式与选取剩下的n-r个元素进行排列的方式是相同的,证明如下:
设A为从n个元素中选取r个元素的任意一个排列,B为剩下的n-r个元素的任意一个排列,那么A和B组合起来就是一个完整的从n个元素中选取r个元素的排列,反之亦然,因此P(n, r) = P(n, n-r)。
性质二:P(n, r) = rP(n-1, r)
这个性质表明从n个元素中选取r个元素进行排列的数目等于先从这n个元素中去掉一个(假设为第n个),再从剩下的n-1个元素中选取r个进行排列的数目乘以r(因为第n个元素可以放在任何位置),证明如下:
考虑第一个位置上的元素有r种选择(即从剩下的n-1个元素中选),接着第二个位置上又有r种选择(因为第一个位置已经选了一个),以此类推,直到最后一个位置上只有1种选择(因为前面的位置都已选好),所以总的排列数为r×P(n-1, r)。
五、排列公式的应用实例
实例一:日程安排
假设一个公司有5名员工(A、B、C、D、E),需要安排他们在一周的5天中进行值班(每天只安排一名员工),问有多少种不同的值班安排方式?
这是一个典型的5个不同元素(员工)取5个(值班日)的排列问题,即P(5, 5),根据排列公式P(5, 5) = 5! = 5 × 4 × 3 × 2 × 1 = 120种不同的值班安排方式。
实例二:密码生成
在计算机科学中,生成密码时常常需要组合不同的字符以增加密码的复杂度,假设密码由3个大写字母和2个小写字母组成,且不考虑顺序(但这里我们关注的是“排列”而非“组合”),问有多少种不同的密码生成方式?
首先考虑大写字母的排列P(26, 3),再考虑小写字母的排列P(26, 2),然后将两者相乘得到总的密码生成方式数,实际上在真实应用中会考虑字符的组合而非顺序,但此例旨在展示排列公式的应用。
六、进阶应用与拓展思考
随着计算机科学和组合数学的发展,排列公式的应用范围也在不断扩展,例如在算法设计中的全排列生成、数据加密中的密钥生成、以及在概率论中对事件顺序的考量等,对于非等概率的排列问题(即不同元素被选中的概率不同),虽然不能直接应用上述公式,但可以通过加权或概率调整的方法进行近似计算。
通过本文的探讨,我们不仅理解了排列公式的推导过程及其数学性质,还见识了其在日常生活和科学研究中的广泛应用,数学之美不仅在于其严谨的逻辑和精妙的公式,更在于它能够为解决实际问题提供强有力的工具和语言,正如排列公式所展现的那样,每一个看似简单的数学概念背后都隐藏着丰富的内涵和无限的应用潜力,希望读者在这次探索之旅中能够感受到数学的魅力,并激发对数学及其应用的进一步兴趣和探索精神。

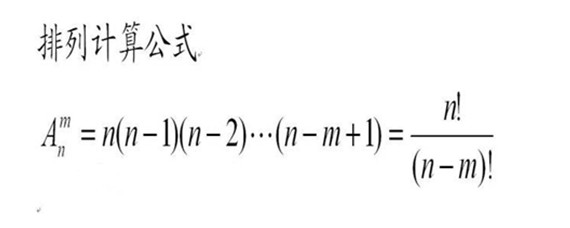
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号